
Making an ICE Chart
An Aid in Solving Equilibrium Problems

Making an ICE Chart
An Aid in Solving Equilibrium Problems
An useful tool in solving equilibrium problems is an ICE chart.
In making an ICE chart the following items should be noted:
Example: A mixture consisting initially of 3.00 moles NH3, 2.00 moles of N2, and 5.00 moles of H2, in a 5.00 L container was heated to 900 K, and allowed to reach equilibrium. Determine the equilibrium concentration for each species present in the equilibrium mixture.
2 NH3(g) ![]() N2(g) + 3 H2(g)
Kc = 0.0076 @ 900 K
N2(g) + 3 H2(g)
Kc = 0.0076 @ 900 K
![]()
|
|
|
|
|
| Initial Concentration (M) |
|
|
|
| Change in Conc. (M) | |||
| Equilibrium Conc. (M) |
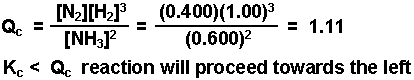
|
|
|
|
|
| Initial Concentration (M) |
|
|
|
| Change in Conc. (M) |
|
|
|
| Equilibrium Conc. (M) |
|
|
|
|
|
| Initial Concentration (M) |
|
|
|
| Change in Conc. (M) |
|
|
|
| Equilibrium Conc. (M) |
|
|
|
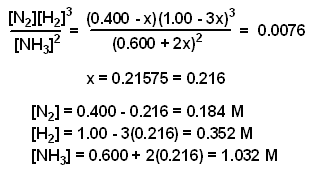
The value of x was determined using the method of successive approximations.
The following examples illustrating writing ICE charts for the problems given. Although each problem appears to be "different" the process for creating the ICE chart is the same.
Example: 4.00 moles of HI are placed in an evacuated 5.00 L flask and then heated to 800 K. The system is allowed to reach equilibrium. What will be the equilibrium concentration of each species?
2 HI(g) ![]() H2(g) + I2(g) Kc
= 0.016 @ 800 K
H2(g) + I2(g) Kc
= 0.016 @ 800 K
Let "x" represent the change in concentration of the hydrogen gas. Since we start
with HI alone, the reaction must proceed to the right resulting in
an increase in the amount of hydrogen gas.
|
|
|
|
|
| Initial Concentration (M) |
|
|
|
| Change in Concentration (M) |
|
|
|
| Equilibrium Concentration (M) |
|
|
|
Only Product Species Are Present Initially
Example: 0.600 moles of NO and 0.750 moles of O2 are placed in an empty 2.00 L flask. The system is allowed to establish equilibrium. What will be the equilibrium concentration of each species in the flask?
2 NO2(g) ![]() 2 NO(g) + O2(g)
Kc = 0.50
2 NO(g) + O2(g)
Kc = 0.50
Let "x" represent the change in concentration of the oxygen gas.
Since only NO and O2 are
present, the reaction must proceed to the left in order to
establish equilibrium. The O2 gas will decrease in concentration over
time.
|
|
|
|
|
| Initial Concentration (M) |
|
|
|
| Change in Concentration (M) |
|
|
|
| Equilibirum Concentration (M) |
|
|
|
Species Added to a System Initially in a State of Equilibrium
Example: The concentrations of an equilibrium mixture of O2 , CO, and CO2 were 0.18 M, 0.35 M, and 0.029 M respectively. Enough CO was added to the flask containing the equilibrium mixture to momentarily raise its concentration to 0.60 M. What will be the concentration of each species in the flask once equilibrium has been re-established after the additional carbon monoxide was added?
2 CO2(g) ![]() 2 CO(g) + O2(g)
2 CO(g) + O2(g)
After the addition of more CO the system is no longer in equilibrium.
The once equilibrium quantities of the other three substances are now initial
quantities. Let "x" represent the change in the amount of O2 gas. Adding
the CO will force the reaction to proceed in the reverse direction (K
< Q) causing the amount of O2 to decrease.
(Note: The equilibrium quantities given in the problem, before the
addition of more CO, are also used to calculate the value of the equilibrium
constant, Kc.)
|
|
|
|
|
| Initial Concentration (M) |
|
|
|
| Change in Concentration (M) |
|
|
|
| Equilibrium Concentration (M) |
|
|
|
Example: Cl2 gas undergoes homolytic cleavage into chlorine atoms at 1100oC. Kp at 1100oC for this process is 1.13 x 10-4. If a sample with an initial Cl2 gas pressure of 0.500 atm was allowed to reach equilibrium, what is the total pressure in the flask?
Cl2(g) ![]() 2 Cl(g)
2 Cl(g)
Let "x" represent the change in the pressure of the Cl2 gas.
Since the reaction will proceed forwards to establish equilibrium the pressure
of the Cl2 gas will decrease. The total pressure at equilibrium
will equal the sum of the partial pressures of each gas at equilibrium.
|
|
|
|
| Initial Pressure (atm) |
|
|
| Change in Pressure (atm) |
|
|
| Pressure at Equilibrium (atm) |
|
|
