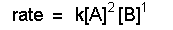Rate Laws from Rate Versus Concentration Data (Differential Rate Laws)
A differential rate law is an equation of the form.
![]()
In order to determine a rate law we need to find the values of the exponents n, m, and p, and the value of the rate constant, k.
- Determining n, m, and p from reaction orders
- Determining n, m, and p from initial rate data
- Determining the rate constant
Determining Exponents for a Rate Law from Reaction Orders
If we are given the reaction orders for a reaction, we have the values of the coefficients we need to write the rate law. For example, if we are told that a reaction is second order in A we know that n is equal to 2 in the rate law.
Determining Exponents for a Rate Law from Initial Rates (Experimental Data)
If we are given data from two or more experiments at the same temperature with different concentrations of reactants and different rates we can determine the exponents in the differential rate law for the reaction as follows:
- Write the rate law with the concentrations of all species for
which data is given. Write the coefficients as unknowns: n, m, etc. For example, we might have an equation such as the following:
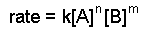
- Take ratios of the experimental data that give different rates.
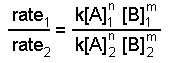
- Cancel common terms and solve for the exponent that does not
cancel.
Example
If we have the following experimental initial rate data for the reaction
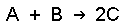
experiment [A], M [B], M rate = -d[A]/dt, M h-1 1 0.50 0.50 1.2 2 1.0 0.50 4.8 3 2.0 1.0 38.4 We can write ratios for the data from experiments 1 and 2
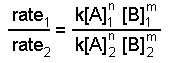
Using the data from experiments 1 and 2, we see that the k's cancel as do the concentrations of species B.
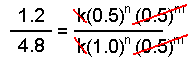
Solving this equation for n yields n = 2.
Now we use the known value of n and data from experiments 1 and 3 or from experiments 2 and 3 and solve for m. Here we use experiments 1 and 3:
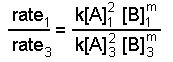
When we substitute the data we get:
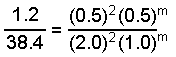
Solution of this equation gives m = 1 and the rate law can be written: