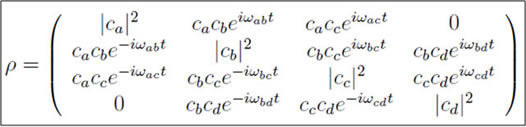Two-dimensional chirped-pulse Fourier transform microwave (CP-FTMW) spectroscopy is used to identify connected rotational energy levels. Rotational transitions that share a common energy level will result in a cross-peak in the 2D spectrum. This technique is similar to 2D correlation methods used in nuclear magnetic resonance (NMR).
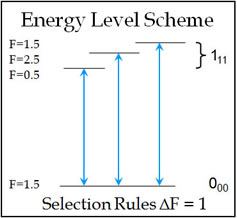In the energy level scheme for 1-chloro-1-fluoroethylene (right), the 111 level is split by the nuclear quadrapole of chlorine. This results in three separate peaks in the rotational spectrum. Because the split 111 levels are connected by the shared 000 level, cross peaks are observed according to the selection rules.
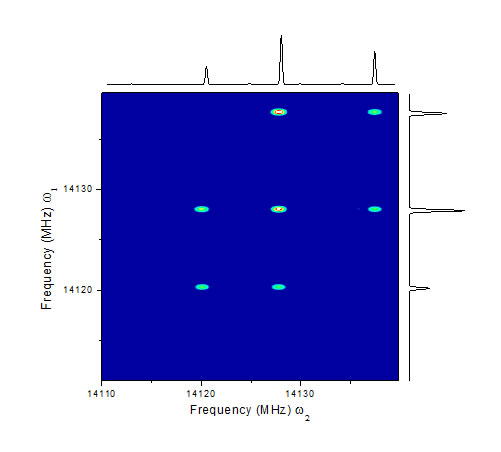In the two-dimensional spectrum of 1-chloro-1-fluoroethylene, the correlation peaks are revealed by taking the Fourier transform in the second dimension. After zooming in along the z-axis, the 13C species are observed in natural abundance (green). The correlation cross peaks of an excited vibrational state of the most abundant isotopomer are also present (red).
Theory
The pulse sequence use for the 2D autocorrelation experiment is made up of two polarizing microwave pulses separated by a delay t1. During the pulses, the evolution of the coherently prepared states can be described by the Liouville-von Neumann equation.
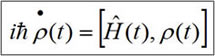
During the t1 delay, each coherence precesses at its resonant frequency, changing the initial conditions for the next pulse with each step. The interference effects are observed as a change in the peak intensity as a function of t1.
For a 4-level purely progressive system, the Hamiltonian matrix has the following form. The energy levels are along the diagonal and the off-diagonal elements are the projection of the electric field onto the transition dipole vector.
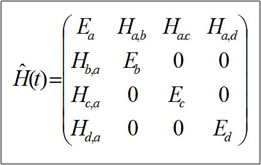
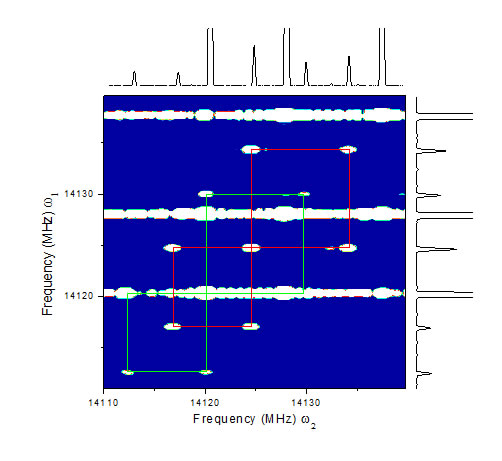
The diagonal elements of the 4-level purely progressive density matrix represent the populations of each state and the off-diagonal terms represent a coherence between two states which oscillates at the resonant frequency of the transition.
