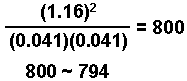Techniques for Solving Equilibrium Problems
- If Possible, Take the Square Root of Both Sides
- Using the Quadratic Equation
- Solving Equations Containing x3, x4, etc.
- The Method of Successive Approximations
- Assume That the Change is Small
Sometimes the mathematical expression used in solving an equilibrium problem can be solved by taking the square root of both sides of the equation. This can be done when the variables in the numerator and in the denominator of the equilibrium expression are multiplied by themselves (squared).
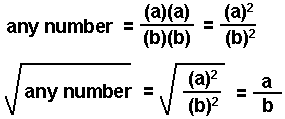
Example:
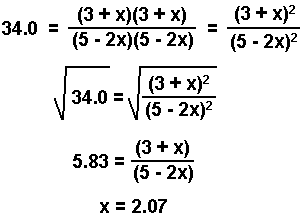
If you can take the square root of both sides you will spend less time in solving an equation!
If you cannot take the square root of both sides of the equation, you can use the quadratic equation for an equation of the form:
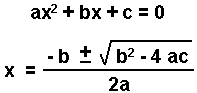
For example:
![]()
- Rearrange to the form: ax2 + bx + c = 0.
- Substitute the coefficients into the quadratic equation and solve for x.
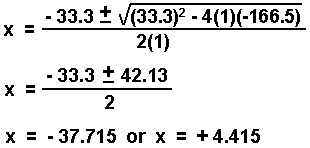
Solving Equations Containing x3, x4, etc.
At times, you will have problems involving equilibrium expressions with the variable "x" raised to a power "n".
xn = a number
With the aid of a calculator there are two ways you can go about solving for x.
The following example will be used to illustrate each method.Example:
(2x)2(3x)3 = 2.4 x 10-18
- Using either method, the first step is to simplify the equation.
- Using logarithms
- Take the log of both sides of the equation.
- Factor out the exponent (log xn = n log x) and find the log of the number.
- Solve for "log x".
- Solve for x (if log x = y, then x = 10y).
- Finding the nth root.
- Most calculators will have a button labeled:
- Enter in the number for which you want the nth root.
- Press the button for finding the nth root followed by the exponent, n, and the "=" or "enter" button to obtain the result.
108 x5 = 2.4 x 10-18
x5 = 2.2 x 10-20
log x5 = log (2.2 x 10-20)
log x5 = -19.66 5 log x = -19.66
log x = -3.93
Often this button is in conjunction with the "yx" button. You may need to push "2ND" or "INV" before the button to find the nth root. Consult the manual that came with the calculator for the exact procedure.
The Method of Successive Approximations
One method of solving what appears at first to be very daunting equations is to:
- assume an approximate value for the variable that will simplify the equation
- solve for the variable
- use the answer as the second apporximate value and solve the equation again
- repeat this process until a constant value for the variable is obtained
![]()
- Approximate a value for the variable that will simplify the equation.
- Simpify the equation and solve for the variable.
- Using the result, make a second approximation.
- Using the second approximation, simplify the equation and solve for the variable
- Repeat the process until a constant value is obtained.
Since 8.4 x 10-4 is a small number, the value of x must be small. We will make the assumption that:
0.200 - x ~ 0.200
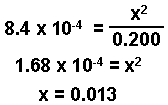
0.200 - x = 0.200 - 0.013 = 0.187
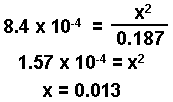
In this example, a consistant value has been obtained after making only two approximations.
There are two special cases where we can solve an equation by assuming the variable is small.
K and Q Are Very Close in SizeWhen K and Q are close to being the same value and are on the same side of 1, the change in amount of each species will be very small as the system moves towards a state of equilibirum. When this occurs, finding the change in concentration can often be facilitated by doing the following:
- Calculate Q, the reaction quotient and compare to K.
- Make an ICE chart.
- Subsitute concentrations into the equilibrium expression. Assume that [A] - x = [A], simplify the equation, and solve for the change.
- Check to see if the change is less than 5% of the starting quantity, or within the limits set by your instructor.
- Calculate the equilibrium amounts if asked to do so.
- Check your work.
Example: Determine the concentration of each species present in a 0.500 M solution of a weak acid HA. HA reacts with water according to the equation:
- Calculate Q and compare to K.
- Make an ICE chart.
- Substitute into the equilibrium expression. Assume that 0.500 - x ~ 0.500. Simplify equation and solve for the change.
- Check answer to see if it is within limits set by your instructor. (Here we use 5%.)
- Determine the equilibrium concentrations of each species
- Check work.
In this example, initially there are no products so Q = 0. K > Q so the reaction will proceed in the forward direction. However, K and Q are < 1. The change in the concentration will be small.
|
|
|
|
|
| Initial Conc. (M) |
|
|
|
| Change in Conc. (M) |
|
|
|
| Equilibirum Conc. (M) |
|
|
|
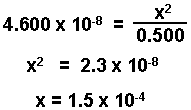
The change is only 0.03% of the initial value and is negligible.
[HA] = 0.500 - 1.5 x 10-4 = 0.500 M
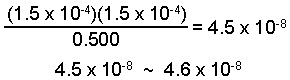
K and Q Lie on Opposite Sides of One (K>>Q or K<<Q)
When K is much larger than Q, or K is much smaller than Q, the change in amount of each species will be very large as the system moves towards a state of equilibirum. When this occurs, finding the change in concentration can often be facilitated by doing the following:
- When K>>Q and K > 1, assume 100% conversion into products, followed by the back reaction to establish equilibrium. When K<<Q and K < 1, assume 100% conversion into reactants, followed by the forward reaction to establish equilibrium.
- Make an ICE chart to determine change and equilibrium quantities starting with those resulting from the 100% conversion.
- Substitute quantities into the equilibrium expression.
- Assume the change is near zero such that "[A] - x" is equal to "[A]."
- Solve for the variable.
- Check to see if the change is less than 5% of the maximum amount, or within the limits set by your instructor. If not, use the method of approximations, a programmable calculator, or other method to solve.
- Solve for the equilibrium concentrations if asked to do so.
- Check your work.
H2(g) + I2(g) ![]() 2 HI(g) Kc = 794 @ 298 K
2 HI(g) Kc = 794 @ 298 K
- Initially the [HI] = 0, so K >>Q and K is > 1. The change in the concentration of each species will be large so we calculate the quantity of product formed assuming 100% conversion.
- Make an ICE chart starting with the concentrations after the 100% conversion.
- Substitute equilibrium amounts into the equilibrium expression.
- Assume the change in the concentration of the product is 0. Substitute into the equation and solve for "x."
- Check to see if the change is within the limits set by your instructor. (Here we use 5%.)
- Calculate the equilibrium concentrations.
- Check work.
100% conversion will result in the formation of 1.24 M HI (1 to 1 to 2 proporation) with neither reactant remaining.
|
|
|
|
|
| Initial Concentration (M) |
|
|
|
| Change in Concentration (M) |
|
|
|
| Equilibrium Concentration (M) |
|
|
|
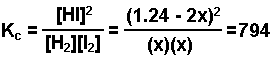
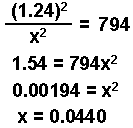
The change in the HI is "2x" or 2(0.044) = 0.088 M
(0.088/1.24) x 100 = 7.1 %
This is greater than 5%. Using one of the other methods of solution (quadratic, successive approximations, or programable calculator) we arrive at:
x = 0.041
[H2] = [I2] = x = 0.041 M
[HI] = 1.24 - 2x = 1.24 -(2)(0.041) = 1.16 M