
Determining Equilibrium Quantities
from Initial Quantities and K
To find the equilibrium quantities of each species from the initial quantities we must know:
- the balanced equation for the reaction
- the equilibrium expression for the reaction
- the value for the equilibrium constant
- the initial quantities of each species, either as molarities, or partial pressures
- the direction the reaction will proceed in order to establish equilibrium
- Write the equilibrium expression for the reaction.
- Check to see that the quantities are expressed in the same units as used in the equilibrium constant.
- Determine the direction the reaction will shift. Calculate Q if direction of shift is uncertain.
- Make an ICE chart and determine the equilibrium quantities in terms of a single unknown change.
- Substitute into the equilibrium expression and solve for the change.
- Calculate the equilibrium quantity for each species from the initial quantity and the change.
- Check your work.
Example: 0.050 mol of H2 and 0.050 mol of Br2 are placed in an evacuated 5.0 L flask and heated to 700 K. What is the concentration of each species in the flask when equilibrium has been established? The equation for the reaction is as follows:
H2(g) + Br2(g) ![]() 2 HBr(g) Kc
= 64 @ 700 K
2 HBr(g) Kc
= 64 @ 700 K
- Write the equilibrium expression for the reaction.
- Since Kc is used in this problem, check to see if the given quantities are in moles per liter (molarity). In this example they are not. A conversion is required.
[Br2] = 0.010 M
[HBr] = 0 M
- The only direction that this reaction can proceed is forward due to the fact that initially there are only H2 and Br2 in the flask. The reverse reaction cannot begin to occur until some HBr is formed.
- Make an ICE chart with "x" representing the change in the concentration of the H2 (or Br2) as the system moves towards equilibrium. All of the other changes are expressed in terms of x.
|
|
|
|
|
| Initial Concentration (M) |
|
|
|
| Change in Concentration (M) |
|
|
|
| Equilibrium Concentration (M) |
|
|
|
- Substitute the expressions for the equilibrium concentrations into the equilibrium expression and solve for "x".
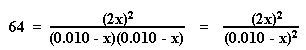
x = 0.008 M
- Calculate the equilibrium concentration for each species from the initial concentrations and the changes.
- Check your answer by substituting the equilibrium concentrations into the equilibrium expression and see if the result is the same as the equilibrium constant.
[H2] = [Br2] = 0.010 - x = 0.010 - 0.008 = 0.002
M for each
[HBr] = 2x = 2(0.008) = 0.016 M
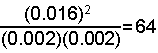
Determining Equilibrium Pressures
Example: 1.000 atm of SO3, 0.150 atm of SO2, 0.200 atm of NO2, and 2.000 atm of NO at 460oC was allowed to reach equilibrium. What is the equilibrium pressure of each gas present in the flask?
SO2(g) + NO2(g) ![]() NO(g) + SO3(g) Kp = 85.0
@ 460oC
NO(g) + SO3(g) Kp = 85.0
@ 460oC
- Write the equilibrium expression for the reaction.
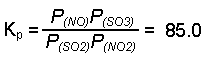
- Since we are using Kp, check to see if the given quantities are in appropriate pressure units (atmospheres). In this example they are, so no conversion is required.
- Calculate the value of the reaction quotient, Q, to determine the direction the reaction will proceed to reach equilibrium.
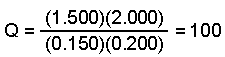
Kp < Q so the reaction will proceed in the reverse direction.
- Make an ICE chart. Let "x" represnt the change in the pressure of the NO. Since the reaction proceeds in the reverse direction, the NO and SO3 will decrease and the SO2 and NO2 will increase as equilibrium is established.
- Substitute the expressions for the equilibrium pressure into the equilibrium expression and solve for "x".
|
|
|
|
|
|
| Initial Pressure (atm) |
|
|
|
|
| Change in Pressure (atm) |
|
|
|
|
| Equilibrium Pressure (atm) |
|
|
|
|
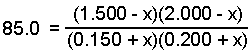
x = 0.013 atm
- Calculate the equilibrium pressure for each gas using the calculated value of x.
PNO2 = 0.200 + x = 0.200 + 0.013 = 0.213 atm
PNO = 1.500 - x = 1.500 - 0.013 = 1.487 atm
PSO3 = 2.000 - x = 2.000 - 0.013 = 1.987 atm
- Check your final answers by substituting back into the equilibrium expression to see if the equilibrium constant is obtained.
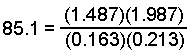
which equals 85.0 within the uncertainty of the calculation.
For more information on the mathematics employed in solving equilibrium problems, click here.
