Maximal Entropy Approach For Quantum State Tomography

Quantum computation has been growing rapidly in both theory and experiments. In particular, quantum computing devices with a large number of qubits have been developed by IBM, Google, IonQ, and others. The current quantum computing devices are noisy intermediate-scale quantum devices, and so approaches to validate quantum processing on these quantum devices are needed. One of the most common ways of validation for an n-qubit quantum system is quantum tomography, which tries to reconstruct a quantum system’s density matrix by a complete set of observables. However, the inherent noise in the quantum systems and the intrinsic limitations pose a critical challenge to precisely know the actual measurement operators that make quantum tomography impractical in experiments. Here, we propose an alternative approach to quantum tomography, based on the maximal information entropy, that can predict the values of unknown observables based on the available mean measurement data. This can then be used to reconstruct the density matrix with high fidelity even though the results for some observables are missing. Of additional contexts, a practical approach to the inference of the quantum mechanical state using only partial information is also needed.

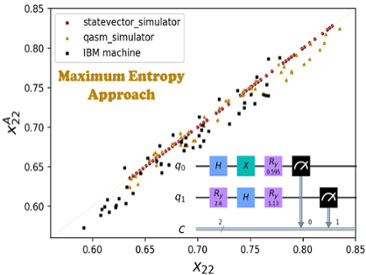
Maximal Entropy Approach for Quantum State Tomography
Gupta, Rishabh; Xia, Rongxin; Levine, Raphael; Kais, Sabre
PRX Quantum 2, 010318 (2021) | PDF

Convergence of a Reconstructed Density Matrix to a Pure State Using the Maximal Entropy Approach
Rishabh Gupta, Raphael D. Levine, and Sabre Kais
J. Phys. Chem. A DOI: 10.1021/acs.jpca.1c05884 | PDF